Regex Engines: History and Contributions
A delightful read on regex, language, reasoning and maths
Regular expressions play an essential role in the history of computing as it is today. This post gives an overview of the evolution of regular expressions - or regex as they are commonly called. Though cryptic in looks, these symbols are quite powerful and can greatly help developers in their daily lives. They are also regarded as one of the least-mentioned successes of standardization in computer science[6]. In this post, we’ll explore the motivations and factors which led to the inclusion of regex as an integral part of programming.
A Mathematical Model of The Brain
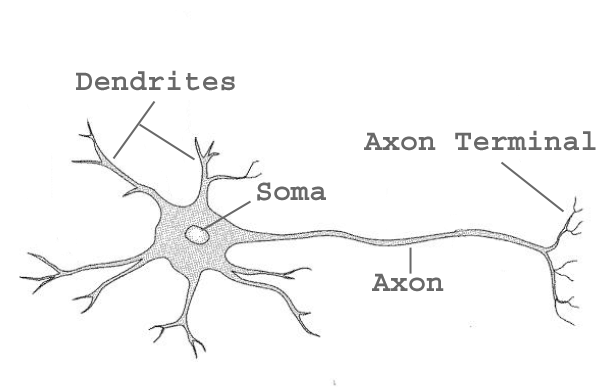
It all starts with a fundamental publication “A Logical Calculus of the Ideas Immanent in Nervous Activity”[0] which translated reads as “A formalization of a meaningful logical theory[1] of the ideas within nervous activity.” It was written in 1943 by Warren S. McCulloch, a neuroscientist, and Walter Pitts, a logician. The paper assumes that the nervous system is a net of neurons, each having a soma and an axon. Here is a simplified illustration [2].
Signals are collected from the dendrites, processed by the soma and output by the axon.
This already looks similar to the perceptron. Signals pass from the axon of one neuron to the soma of another.
A neuron is excited if its threshold is exceeded. It then initiates an impulse.
The paper proposes that since the neurons can be in a firing state or a non-firing state (on or off, which can be represented by 1 or 0), neural events (when neurons fire or not) and the relations among them can be treated by means of propositional logic. A proposition is a statement that can be either true or false. Propositional logic is the branch of logic that studies ways of combining or altering statements or propositions to form more complicated statements or propositions. Though a fundamental paper in the machine learning field, it nevertheless took out from the model the alteration done to the threshold by real life learning. It considered the threshold to be constant and independent of previous learning activity.
One of the conclusions of the paper is that “It is easily shown: first, that every net, if furnished with a tape, scanners connected to afferents, and suitable efferents to perform the necessary motor-operations, can compute only such numbers as can a Turing machine.”
The power of neural networks even at that time was considered remarkable. Von Neumann proposed that any logical, strict and unambiguous description in words can also be described by a neural network [4-1].
Regular Events And Finite Automata
Stephen Kleene in 1951 published a research memorandum for the US Air Force under the umbrella of the famous RAND corporation. It was named “Representation of Events in Nerve Nets and Finite Automata”[3]. It explored the kinds of events a McCulloch-Pitt (nerve) net can respond to by firing an input. Generalizing a net as a finite automaton, it sought to find to what kind of events the finite automaton can respond to, assuming some of its states. It was projected that the results be applied to robotics (robotology as it was called) concerning the pre-programming of its initial states.
The McCullough-Pitt (MCP) paper is closely related to biological neurons. Kleene abstracted away many biological details at that point, as neurophysiology was not in a position to shed light on the real mechanisms of the brain. Among others, the exact firing pattern and delving into circular nets were discarded. The paper defined an event as any property of the input neuron. Even if human life is finite, there is a need for indefinite events. For example, treating a span of 60 years in a human’s life as a chain of events is incredibly long if an event occurs at a delay of 0.005 seconds. And complex, if the events themselves are complex. Explaining behavior in terms of events is an incredible task.
That’s why regular events are introduced. It is more productive to consider events occurring during a time interval. ”We assume for the purpose that the events refer to the inputs up through time p on a set of k input neurons N1 … Nk the same for all events considered”. It showed that all and only regular events can be represented by nets or finite automata. An MCP net can be mapped into a finite automaton by having 2 states (of firing and non-firing, 1 or 0) for the automata’s input cell. The paper concludes with “The Turing machine could be thought of as a finite automaton, which is also able to store information in the environment and reach for it later, so that in certain cases the inputs are identified with inputs at earlier times or with states or certain inner cells at earlier times, and thus the present input is not entirely independent of the past.”
Thinking in terms of finite automatons helped bridge the gap between brain and computer sciences. The term “regular expressions” does not appear in the memorandum, but it does appear in the print published in Automata Studies in 1956 [5]. The first occurrence is in the form “In writing expressions for regular sets or the events they describe …” until finally written under a table “Algebraic transformations of regular expressions”. Kleen introduced operators to represent regular events A + B (or union), A ◦ B (or concatenation), and A* (or the “Kleene Star” or iterate)
Regular expressions became the notation for describing the functioning of finite automatons. For some time thereafter the term “regular events” was synonymous with “regular expressions” such as in “Transition graphs and the star height of regular events” (1963)[8]. The term remains in use with the last known appearance as late as 2001.
Finite Automata For Improving Lexical Processing
Technically speaking the history of the inception of regex ends here. But, it is interesting to view the development of the notations and earliest uses of the concept. In 1968 Douglass Ross et al. published a paper describing the RWORD system called “Automatic Generation of Efficient Lexical Processors Using Finite State Techniques”[7]. The system was designed to let users describe the lexical properties of their language.
The program changed state as each character was read. They interchanged the word events to mean a string of characters. The system was then a decision-making machine based on an ordered sequence of events. A language like this
BEGIN
S(1) = B/AS,
S(2) = AS,
S(3) = A/C$,
END FINI
produced this kind of finite-state machine.
Regular Expressions For Search And Substitution
Around 1968, Ken Thompson (Unix paper co-author) introduced regular expressions [10] for use in an interactive text editing program [11]. The QED (Quick EDitor) editor was in use at Berkeley where Ken worked before coming to Bell Lab. He rewrote the editor using the IBM 7090 assembly language with the notable introduction of regex to match substrings for substitution. Older editors supported literal search. During Bell Lab’s participation in the Multics project, Ken (as genius as always) rewrote the editor this time using the BCPL language. Language B was a mutation of this language and C was based on language B. The BCPL implementation did not compile regex to machine code but instead used trees as representation. After Bell Lab’s withdrawal from Multics, Dennis Ritchie rewrote the editor using assembly language again. The regex inclusion was a pioneering idea as well as the execution model.
Here are the rules Ken followed [11]:
<nl> means new line.
An ordinary character is a regular expression which matches that character.
“^” is a regular expression which matches the null character at the beginning of a line.
“$” is a regular expression which matches the null character before the character (usually at the end of a line)
“.” is a regular expression which matches any character except <nl>
“[<string>]” is a regular expression which matches any of the characters in the <string> and no others.
“[^<string>]” is a regular expression which matches any character but and the characters of the . q) A regular expression followed by “*” is a regular expression which matches any number (including zero) of adjacent occurrences of the text matched by the regular expression.
Two adjacent regular expressions form a regular expression which matches adjacent occurrences of the text matched by the regular expressions.
Two regular expressions separated by “|” to form a regular expression which matches the text matched by either of the regular expressions.
A regular expression in parentheses is a regular expression which matches the same text as the original regular expression. Parentheses are used to alter the order of evaluation implied by g), h), and i) : “a(b|c)d” will match “abd” or “acd”, while “ab|cd” matches “ab”or “cd”.
If “<regexp>” is a regular expression, “{<regexp> x}” is a regular expression, where x is any character. This regular expression matches the same things as <regexp>; it has certain side effects as explained under the Substitute command.
If <regexname> is the name of a regular expression named by the E command (below), then “\E<regexname>” is a regular expression which matches the same things as the regular expression specified in the E command. More discussion is presented under the E command.
The null regular expression standing alone is equivalent to the last regular expression encountered. Initially the null regular expression is undefined; it also becomes undefined after an erroneous regular expression and after use of the E command.
Nothing else is a regular expression.
No regular expression will match text spread across more than one line.
And he gave some examples:
/abcd/ matches “abcd” anywhere in a line.
/ablcd/ matches “ab”or “cd” anywhere in a line.
/ab*c/ matches “ac”, “abc”, “abbc”, “abbbc”, …
/^begin/ matches “begin” at the beginning of a line.
/end$/ matches “end” at the end of a line.
/^begin.*end$/ matches any line beginning with “begin”and ending with “end”.
/^$/ matches an empty line.
/abc[1234567890]/ matches “abc” followed by a digit.
/abc[^1234567890]/ matches “abc” followed by a non-digit.
Ken published “Regular Expression Search Algorithm” describing the approach he used. When confronted with a dubious choice in pattern-matching, regular expression engines can either look ahead or backtrack or use parallelism to explore several choices at the same time. This paper, one of the earliest on the subject, surprisingly took the parallel approach. He might have been influenced by “Multiple-Paths Syntatic Analyser”[23], a linked paper. It remains efficient even when compared to many later engines [22]. The implementation takes in a regular expression as source language and outputs IBM 7094 code which is then compiled as a program and executed on the source string to find all substrings.
The search used a non-deterministic finite automaton approach. A non-deterministic automaton allows many states to move next. The theory and motivation behind the endeavor to create a well-grounded program come from Janusz Brzozowski who presented a great method for constructing a recognizer from a regular expression based on regular-expression derivatives [24].
Eventual Popularity
Considering both the program and the syntax, Ken Thompson’s program was the first proper engine, though being a first attempt. Grep, as a unix utility, was a more powerful tool than the editor search feature. The grep flavor is known as BRE. Egrep, written by Aho was an improvement over the latter and has supported extended regex (ERE). Rob Pike from Bell Lab (funny isn’t it) while working on the Sam editor (history strikes twice), developed a language to make tasks easy to specify [15]. He used regex to describe the structure of the text being modified. He used Ken’s forgotten algorithm but, instead of on-the-fly compilation, interpreted the regex. It used an egrep flavour.
Regex libraries started to gain traction around the 1980s. Henry Spencer in 1986 [17] wrote and distributed his libraries[12]. The oldest one adopted the egrep flavour and was a revision of his regexp(3) library[13]. Subsequent ones were the BSD library and the TCL library. The 8.1 release of TCL included among others new backslash notations like \d for digits [14]. Larry Wall adapted Spencer’s library [17] for inclusion in Perl in 1988 [18][19] to improve the existing regex [20]. In 1997, Jeffrey Friedl’s book “Mastering Regular Expressions” became wildly popular.
Around the same time, Philip Hazel was looking for a regular expression library. He considered Spencer’s library to be limited and Perl’s adaptation too tightly bound. He went on to create the Perl Compatible Regular Expressions (PCRE) engine, written in C. It saw light in a new release of the Exim mail software. The software proved to be so successful as a library of it’s own that in 2008 Exim stopped shipping its own version of the lib. PCRE2 development continues to this date and features JIT support. Both PCRE and Perl used the backtracking method. Funnily enough, Hazel coded his algorithm in IBM Assembler in order to add regular expression support to the ZED text editor. It was re-implemented in BCPL and then in C for the E and NE editors that succeeded ZED. Editors it seems, played a great role in propelling regex as a language of convenience.
Later Pearl versions added even more features.
The Background of Formalizing Languages: Syntax and Logic
The foray of McCullogh-Pitts into representing nerve nets using propositional logic has deeper roots in the thoughts of Rudolph Carnap. They listed The Logical Syntax of Language[21] from Carnap as a reference paper without linking parts of their paper or explaining its relevance. McCullough explains it’s relevance at the end of Von Neumann’s lecture on Automata [27].
McCullogh had interest in Mathematics and Philosophy. He entered into psychology to understand how mathematics could arise from the biological sphere. He entered physiology to get better answers. In 1919 he tried to construct a logic for transitive verbs by formulating it as a problem of modal logic. It was not the right start, but it was a point of inception. Turing’s paper gave him some ideas to visualise the brain as a turing machine. He then came up with the theory of how neural nets can be used to compute any number. He related neural signals to a logical input, which Kleene described more elegantly. Since the initial base of McCullogh was connected with languages (verbs) and since they maintained it’s relevance in their paper by linking it to Carnap, it’s interesting to have an idea of what Carnap’s paper was about,
In “The Logical Syntax of Language”, by “logical syntax” Rudolph means stating the formal rules which govern language and developing the rules which follow as a consequence. It’s propositional logic in another fashion. Carnap explains that logical characteristics of the language (affirmation, contradiction, …) and the logical relationship between them are dependent on the syntactical structure of the sentences. In this way he states, “logic will become part of syntax provided that the latter is conceived in a sufficiently wide sense and formulated with exactitude”. Though referring to natural languages, he points out that to undertake this task using these languages is not feasible due to non-uniformity and arbitrary rules. Instead, he proposed constructing from symbolic, artificial languages. There are two languages: object-languages for the language being described and the syntax-language for transcribing the rules.
Interestingly enough we encounter many compiler-related jargons. It defines a calculus as a system of “rules” having elements called “symbols”, whose finite series is called an “expression”. We also see in it Kleene’s exploration concerning the relationship between initial states and events. It is illustrated in the paper by a game of chess. The game is a calculus, the chessmen, symbols (meaningless in this case), the rules of formation dictate their positions especially the initial states and, the rules of transformation describe valid moves.
If a language has the attributes of a calculus, it can be treated and manipulated in the same way as a calculus. The logical methodology of science is the syntax of the language of science. Languages share common concepts and an underlying structure. A mock language can be cooked up based on these and rules are then applied to this language. Metamathematics is an attempt to treat mathematics as a calculus, rules having mathematical formulae for what they describe so as to obtain the proof that classical mathematics is free from contradiction. In the same way, treating language as a calculus can provide a way to detect contradictions in natural languages.
In a discussion of formalizing languages, illustrations are given and references to programming language concepts crops up. For example, adjectives of cold, warm etc for example can be reduced to numbers such that temp(3) = 5 means temperature at position 3 is five. This is called a functor. In the expression sum(3, 5), 3 and 5 are parameters and 5 is the value of sum(3,5). It can also be used for any concept such as temp(3) = 5. It also defines numerical variables as x, y, z … . It goes on to define a constant as a symbol that is not a variable, predicates using capital letters, and numerical constants as 1, 2, 3, 4. It also constructs truth tables. Sentences are then given classifications such as derivable, contradictory, etc. He proposes that everyone is at liberty to create their own languages as long as they state their methods clearly and give their syntactic rules. This was proposed as early as 1934.
The crux of these discussions can be seen in the usage of regular expressions to describe formal languages which is an expression of computer languages. Carnap’s paper is a treatise on mathematics and philosophy. Over time, regular expressions as Kleene described them were used in language theory in conjunction with mathematical concepts such as sets. The regex (0 + 1)* for example, is the set of all binary strings. This is how regex became the plaything of both mathematicians and computer scientists.
[26]
Conclusion
Over time, programming languages started shipping regex modules as part of their standard library. Regex are super efficient at identifying patterns. There have been many other variations of pattern matching languages, like COMIT, SNOBOL and FLIP. But, in terms of ease, conciseness, integration and closeness as is to maths, regex is hard to beat!
Notes
Thanks to the Metabob team for reviewing.
Thanks to Russ Cox for a beautifully written article about regex, and Christopher M. Kelty for producing a most delightful read.
References
[0] A Logical Calculus of the Ideas Immanent in Nervous Activity (McCulloghPitt, 1943)
[1] https://encyclopediaofmath.org/wiki/Logical_calculus
[2] An Open Domain-Extensible Environment for Simulation-Based Scientific Investigation (ODESSI) - Scientific Figure on ResearchGate. Available from: https://www.researchgate.net/figure/The-main-structur-of-a-neuron-consists-of-soma-dendrites-and-axon_fig3_220856618
[3] Representaion of Events in Nerve Nets and Finite Automata [RAND project, RM-704] (Stephen Kleene, 1951)
[4] The General and Logical Theory of Automata (John Von Neumann, 1948)
[4-1] “McCullock and Pitts’ important result is that any functioning in this sense which can be defined at all logically, strictly and unambiguously in a finite number of words can also be realized by such a formal neural network”
[5] Representaion of Events in Nerve Nets and Finite Automata, Automata Studies [Annals of Mathematics Studies, Number 34, Princeton U. Press, Princeton, N.J] (S. Kleene, 1956)
[6] Speech and Language Processing: An introduction to natural language processing,
computational linguistics, and speech recognition (Daniel Jurafsky & James H. Martin, Draft Dec 2020)
[7] Automatic generation of efficient lexical processors using finite state techniques [Communications of the ACM 11.12 - 805-813] (Johnson, Walter L. et al., 1968)
[8] Transition graphs and the star height of regular events, Michigan Math (L. C. Eggan, 1963)
[10] An incomplete history of the QED Text Editor https://www.bell-labs.com/usr/dmr/www/qed.html
[11] Cover Sheet Technical Memorandum for The QED Editor https://www.bell-labs.com/usr/dmr/www/qedman.pdf
[12] https://garyhouston.github.io/regex/
[13] https://github.com/garyhouston/regexp.old
[14] https://www.tcl.tk/doc/howto/regexp81.html
[15] https://web.archive.org/web/20040308012826/http://plan9.bell-labs.com/sys/doc/sam/sam.html
[16] https://garyhouston.github.io/regex/
[17] From Punched Cards To Flat Screens, A Technical Autobiography (Philip Hazel) https://drive.google.com/file/d/10TAOEgIL--CmzqOl0fkdP-cagjSLBM4J/view
[18] https://www.shlomifish.org/perl-timeline-temp/PerlTimeline.html
[19] https://github.com/rhaamo/perl2/blob/0a4f4405aaebfbf10f12e28f0e7cec514352d6e2/Changes#L1
[20] https://github.com/AnaTofuZ/Perl-1.0
[21] Logical Instruments: Regular Expressions, AI and thinking about thinking (Christopher M. Kelty, 2008) https://kelty.org/or/papers/Kelty_Franchi_LogicalInstruments_2009.pdf
[22] Regular Expression Matching Can Be Simple And Fast (Russ Cox, 2007) https://swtch.com/~rsc/regexp/regexp1.html
[23] The Logical Syntax of Language (Rudolph Carnap, 1934)
[24] Multiple-Paths Syntatic Analyser (S. Kuno et al., 1962)
[25] Derivatives of regular expressions. (J. Brzozowski, 1964)
[26] Regular-expression derivatives reexamined (Owen et al.)
[27] The General and Logical Theory of Automata (John Von Neumann)










Woo! I don't imagine the time it took you to write this, well done!