Step By Step Parsing of Mathematical Expressions From Scratch
Illustrated guides to become better programmers
Were you to write your own language, one difficulty which requires a different twist is parsing mathematical expressions. Maybe if you thought about it hard enough you could derive it from scratch but it’s worth it to learn standard techniques. As always, this post hopes to be simple enough for a teenage coder to understand, follow along and implement. Promise.
What do maths expressions mean?
Some maths libraries are able to parse expressions like this one: sin(1)+2. But, for this post, we’ll bind ourselves to expressions of this sort: 1+2-(3*2)**10/4. It’s just to enable us to focus on solving this post's challenges as we can delegate function calling to the language itself.
General Challenges
We must verify that the brackets match.
We must identify the correct operator. Here we are implementing ** to mean power of.
We can also add white-space insensitiveness etc but we’ll divert from the topic.
Balancing parenthesis
Balancing parenthesis is easy. We use an array/list/stack.
When we encounter an opening parenthesis, we add it to the stack.
When we see a closing parenthesis, we remove it from the stack.
And so on
Error situations look like these
Here’s a Python implementation of it
For general balancing, just replace `if char == ‘(‘` by if char in `’({[’` and do the same for ‘)’ and ‘)}]’.
Identifying the correct operator
To ease parsing, we parse in two steps. The first one identifies the symbols and the second one does the evaluation.
To differentiate between * and **, we just see whether the next character is a *. (link)
We haven’t added the balanced parenthesis check for clarity. The snippet outputs
['111', '+', '2', '+', '(', '33', '**', '2', ')', '-', '1', '*', '1']
It correctly separates numbers and operators. Here’s how it works.
and so on …
Converting to postfix notation
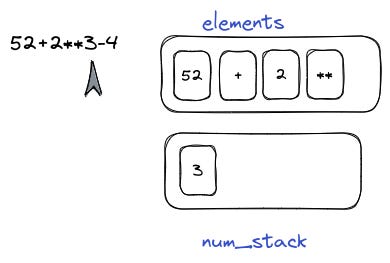
Now that we can identify our elements, let’s actually evaluate them.
One way of doing so is to convert our expression to postfix. Then evaluate it in that form. The postfix form or reverse polish notation form removes the need to have brackets.
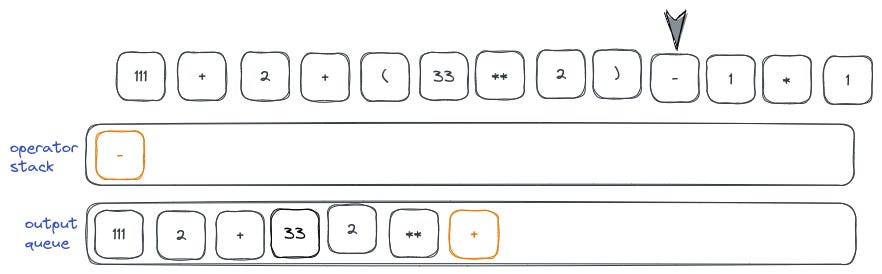
One way to do it is to implement the shunting yard algorithm. It’s just a way to deal with simulating brackets based on operator precedence. It looks a bit like this.
Here’s a Python implementation of it (link).
Here’s how it plays out, step by step
Evaluating postfix notation
Evaluating the postfix expression is very straightforward.
The answer will be the value left in the stack.
Here’s a Python implementation (link).
Glad you made it this far! You deserve to treat yourself to a nice breakfast!
Exercise
We derived the code for checking for parenthesis but did not use it. Add it.
Add more checks. Deal with whitespace.
Notes
Resources on the internet are pretty poor. For the shunting yard algo for example, many tutos did not cover all cases.
There are more ways to evaluate expressions. Using trees for example. You don’t even need postfix. But, postfix is simpler to visualize and understand.
We also choose to devote a section dedicated to identifying elements in the expressions. That way we can add operators like <<.